Current Projects

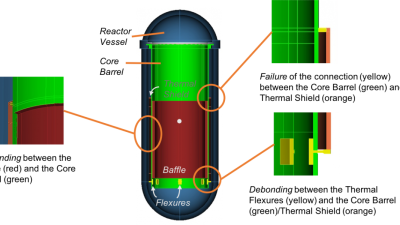
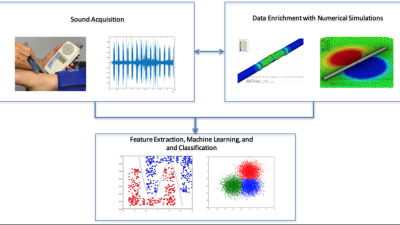
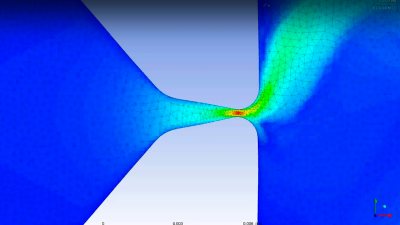
Welcome to the Inverse Problems and Optimization in Mechanics (IOMech) Lab!

Our Main Research Areas are:

  • Computational Mechanics & Inverse Problems
  • Design & Control
  • Optimization & Uncertianty Quantification
  • Medical Imaging

IOMechLab Current Projects and associated research areas are listed below:

Filter by Research Areas

CPS: Medium: Collaborative Research: Smart Ultrasound ELAS

Title: CPS: MEDIUM: COLLABORATIVE RESEARCH: SMART ULTRASOUND ELAS Sponsor: National Science Foundation Period: 10/1/2018-9/30/2021 PI: Michael Zavlanos Co-PI: Wilkins Aquino, Miroslav Pajic, and Mostafa Fatemi IOMechLab Research Scientist: Reza Khodayi-...

Hip Undeformed Standing

FAIS - Model-Based Surgical Planning for FAIS

Title: FAIS - Model-Based Surgical Planning for FAIS Period: Ongoing PI: Wilkins Aquino, Richard Mather III IOMechLab Students: Max Nezdyur The goal of this project is to develop a framework for surgical planning of Femoroacetabular Hip Impingement...

Generalized Methods for Computing Residual Stress

Title: Residual Stress Sponsor: Sandia National Laboratories Period: 2017-2020 PI: Wilkins Aquino IOMechLab Students: Mark Chen In this project, we develop a generalized residual stress inversion technique capable of being applied on any...

Reactor Vessel Damage

GUARDIAN: General Active Sensing for conDItion AssessmeNt

Title: GUARDIAN: General Active Sensing for conDItion AssessmeNt Sponsor: DOE-NEUP Period: 7/1/2019-6/30/2022 PI: Wilkins Aquino Co-PIs: Michael Zavlanos, Timothy Walsh (Sandia), Gregory Banyay (Westinghouse) IOMechLab Students: Mark Chen The goal...

Classification of Peripheral Arterial Disease

Machine Learning Strategies for Classification of Peripheral Arterial Disease in Lower Extremities

Title: Machine Learning Strategies for Classification of Peripheral Arterial Disease Period: Ongoing PIs: Wilkins Aquino, Leila Mureebe IOMechLab Students: Mark Chen The goal of this project is the development of a new paradigm for intelligent...

Arterial Simulation

Measuring Arterial Material Properties using Wave-based Approaches with Ultrasound and Computational Models

Title: Measuring arterial material properties using wave-based approaches with ultrasound and computational models Sponsor: NIH Period: 1/1/2020-12/31/2025 PIs: Matthew Urban, James F Greenleaf (Mayo College of Medicine), Wilkins Aquino (Duke...

fluid-structure interaction (FSI) model of the human vocal folds

Modeling & Control of the Human Voice

Title: Modeling & Control of the Human Voice Sponsor: National Institutes of Health Period: 2019-2023 PI: Dennis Frank-Ito  Collaborators: Wilkins Aquino, John Dolbow  IOMechLab Students: Max Nezdyur The objective of this project is to...

sand particles

Novel Techniques for Topology Optimization

Title: Novel Techniques for Topology Optimization Sponsor: Department of Energy (CSGF) Period: 2015-2020 PI: Wilkins Aquino IOMechLab Students: Clay Sanders, Lourdes Reyes We are developing novel topology optimization approaches for vibration...